'Traffic Congestion' As Solvable, Part 1
In which I outline a framework for evaluating traffic congestion as nothing more than a mismanaged resource that ought to be managed rightfully
Every time I am driving a car and sit in traffic, I feel viscerally frustrated. I know this is true for many people.
Dear humans of the world. Your frustration is well founded. When you sit in traffic, you can and should be directing your ire at someone. Not the other drivers on the road, no, it’s not their fault.
Direct your ire at your cities zoning staff, and your city’s engineering staff.
Both of these roles participate in coercing upon the world pseudo-scientific overlays of a regime that perpetuates great harm in the world.
Not the least of this harm is in the form of the time-sink of sitting in traffic, the opportunity cost of that time, and the enormous pollution coming from these cars.
Oh, and the huge number of accidents that happen in/around rush hour. The incredible numbers of vehicle miles traveled as workers commute from business districts where they work to far-flung suburbs where they try to live as cheaply as possible.
But don’t even hate (necessarily) the planners of today. Hate the planners from the 50s that used those highways to support ethnic cleansing, by running highways through ethnic enclaves.
Anyway, lets stop with the pseudo-science and move with real science.
I’ve got a bunch of written notes about this, so lets go.
This is part 1 of an ongoing series. Part 2: about intersection space consumption, and meditations on evaluating vehicle speeds.
Build from first principles
1. What’s the vehicle carrying capacity of a single lane
Imagine a single lane, the length of a city block. Actually, don’t imagine it, just look at this random block with parked vehicles from the Rino/River North district of Denver.
Would you agree that there is a number, that could be determined, for how many vehicles fit in this lane?
Every evaluation, measurement, and treatment I’m about to recommend can be done on pretty much any road segment. We’re dealing with something simple to exemplify a principal
How many cars could fit in a lane, the length of this block?
We can see how many cars could fit on the lane if they were all parked. There’s plenty of cars already parked, and we’ll do some educated guessing for the rest.
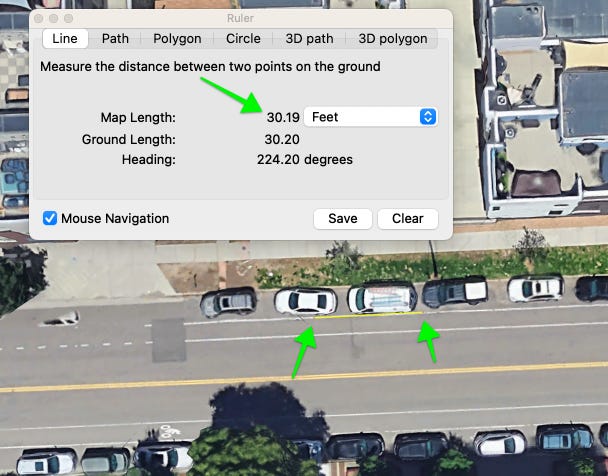
We’re going to ‘do math’ on a single lane. I’m using Google Earth’s built-in distance measuring tool for all of these figures. You could do the same.
This block is about 412 feet, end of the yellow line to the end of the yellow line. Lets round that to 410’.
Next, how much space is consumed by a parked car/truck/van?
These vehicles are all parallel parked, some more tightly than others, but it seems reasonable to assume this density. I measured four cars, and the length is 80 feet. So lets say a stationary, parallel-parked car takes ~20 feet.
So, this 410’ block has a maximum ‘carrying capacity’ of (410/20) 20.5 cars.
But we’re talking about mobility networks here, so we have to assume that if cars are using a lane, they’re trying to go somewhere, they’re moving.
Here’s the kicker - cars consume more space when they’re moving. I know, I know, bonkers! Lets get after it.
2. What’s the vehicle carrying capacity of a single lane at a vehicle speed of ten miles per hour
When driving, for safety, people tend to leave two or three seconds between them and the vehicle ahead. At lower speeds, two seconds makes sense. Breaking distance increases geometrically with a linear increase of speed, so if you’re going ‘fast’, more distance becomes necessary.
For low speeds, we’ll assume a two second gap between moving cars.
At 10 mph, one would be covering 14.6 ft per second. Lets round that to 15 feet.1
Therefore, at two seconds distance between vehicles, there would need to be 30 feet between the rear bumper of the front car, and the front bumper of the rear car.
Here’s what that might look like, approximately. Measuring 30 feet from the front bumper of the black truck:
The truck has a length, of course, so to figure out the distance consumed by a car at 10mph, one would add the travel distance + vehicle length:
How convenient, 50 feet. This is a close-enough rule of thumb. at 10mph, one car can fit every 50 feet of road length.
So how many cars would fit on this road segment at 50 feet each?
410/50 = 8.2
Here’s what that looks like. Each polygon is a 50’ space. I measured each spot with the ruler, then filled in a polygon to the same dimension. It’s a static image, but imagine a car at the right side of each shape, moving to the left, at 10mph. This is the approximate spacing.
When’s the last time you went 10 mph in a car? It doesn’t happen a lot, and I’m obviously opinionated, I’m going to advocate in the next episode of this series aiming for a free-flow movement pattern of 20 mph throughout a given geographic region.
That means we’ll need to add up all non-intersection road segments, and ‘do math’ on assuming a 20mph vehicle speed, and the amount of space consumed by a vehicle at that speed.
3. Determining a ‘vehicles per lane’ carrying capacity at 20 mph
Lets re-do this with a 20mph. At 20mph, a vehicle covers 30 feet per second. Two seconds of travel time between vehicles means 60 feet between, plus the actual vehicle length of 20 ft. (A Toyota Tacoma is almost 19 ft long, a Corolla is 16 feet long, 20 feet is close enough for me)
So, at 20 mph, a vehicle will consume (60 ft between vehicles) + (20 ft of vehicle) = 80 feet of lane distance.
Lets reexamine the same sized block at 80 feet per vehicle:
This is a block one block south. It looks different, you can see that Denver’s Department of Transportation and Infrastructure attempted some pedestrian affordances with the paint. Paint isn’t infrastructure, so it doesn’t count.2
Anyway… at 20mph, a single ‘long’ block in Denver can accommodate five vehicles.3
At 20mph, you’d add up the total lane feet, divide by 80, and that’s the number of vehicles that could be supported in that space, before the network becomes over-burdened and congested.4
That’s 66 vehicles per mile of lane, by the way, at 20 mph.
Next time you’re on a highway, consider that 60 mph consumes 88 ft per second, and we’re gonna bump the travel distance to 3 seconds between vehicles, because it’ll take you longer to stop at such high speeds. At this speed, a vehicle consumes 290’5.
4. Carrying capacity at 40 mph
I’m rounding 88’ per second to 60’, * 3 seconds + 20 feet of vehicle length = 200 ft
Here’s what 200 ft per vehicle looks like, which is what a vehicle would consume at 40 mph:
Just for fun, so you can see the catastrophic difference between space consumption appropriate for urban regions vs. rural highways, here’s space consumed at 60 mph:
Summary
OK, here’s the end of part 1. I perceive this to be an apprehendable explanation of how to think of ‘space consumed per vehicle’ at a given speed.
Here’s a written summary:
10 mph/2 seconds between: 50 ft
20 mph/2 seconds between: 80 ft
30 mph/2 seconds between: 110 ft
40 mph/3 seconds between: 200 ft
50 mph/3 seconds between: 245 ft
60 mph/3 seconds between: 290 ft
Here’s the visual summary, clockwise top right, 10mph, 20mph, 40 mph, 60 mph:
Next time, junctions (link to part 2). We’ll talk about how to calculate flow rate for a given intersection, regardless of it’s busy-ness, configuration, style. Intersections/junctions are not complicated, but they are complex, it might take two episodes to properly address them. (Update, it will certainly take at least two posts to properly address them.)
Once we have shared conceptual understanding of:
vehicles per lane segment at {speed}
flow rate/throughput for a given intersection
We’ll be in an interesting position regarding the inferences we can draw.
Until next time,
-❤️, Josh
I apologize for the imperial unit usage, to any reader of the global majority. I’ll perhaps go back and do a transliteration into metric units soon.
If they’d scribed these shapes with bollards, I’d give them full credit. Flex-posts are propaganda, and are worth somewhere between “nothing” and “worse than nothing”.
We’ll talk about intersections next edition. Some of you might already be thinking about my claim for ‘arbitrary free-flowing traffic at 20mph’, and then thinking about stop signs, traffic lights, left turns, arterials, and more. In this piece, I’m simply explaining a heuristic for calculating the carrying capacity of a given region with a certain total lane-feet.
Congestion is viewed by serious people as ‘a failed state’, similar to a website returning a 404 or 403 error, and on principle I reject that it needs to happen.
Stopping distance grows exponentially, not linearly, with speed.